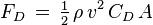In fluid dynamics, the drag equation is a formula used to calculate the force of drag experienced by an object due to movement through a fully enclosing fluid. The formula is accurate only under certain conditions: the objects must have a blunt form factor and the fluid must have a large enough Reynolds number to produce turbulence behind the object. The equation is
where
- FD is the drag force, which is by definition the force component in the direction of the flow velocity,
- ρ is the mass density of the fluid,
- v is the velocity of the object relative to the fluid,
- A is the reference area, and
- CD is the drag coefficient – a dimensionless coefficient related to the object's geometry and taking into account both skin friction and form drag.
The equation is attributed to Lord Rayleigh, who originally used L2 in place of A (with L being some linear dimension).
The reference area A is typically defined as the area of the orthographic projection of the object on a plane perpendicular to the direction of motion. For non-hollow objects with simple shape, such as a sphere, this is exactly the same as a cross sectional area. For other objects (for instance, a rolling tube or the body of a cyclist), A may be significantly larger than the area of any cross section along any plane perpendicular to the direction of motion. Airfoils use the square of the chord length as the reference area; since airfoil chords are usually defined with a length of 1, the reference area is also 1. Aircraft use the wing area (or rotor-blade area) as the reference area, which makes for an easy comparison to lift. Airships and bodies of revolution use the volumetric coefficient of drag, in which the reference area is the square of the cube root of the airship's volume. Sometimes different reference areas are given for the same object in which case a drag coefficient corresponding to each of these different areas must be given.
For sharp-cornered bluff bodies, like square cylinders and plates held transverse to the flow direction, this equation is applicable with the drag coefficient as a constant value when the Reynolds number is greater than 1000.For smooth bodies, like a circular cylinder, the drag coefficient may vary significantly until Reynolds numbers up to 107 (ten million).
The equation is based on an idealized situation where all of the fluid impinges on the reference area and comes to a complete stop, building up stagnation pressure over the whole area. No real object exactly corresponds to this behavior. CD is the ratio of drag for any real object to that of the ideal object. In practice a rough unstreamlined body (a bluff body) will have a CD around 1, more or less. Smoother objects can have much lower values of CD. The equation is precise – it simply provides the definition of CD (drag coefficient), which varies with the Reynolds number and is found by experiment.
Of particular importance is the 
dependence on velocity, meaning that fluid drag increases with the square of velocity. When velocity is doubled, for example, not only does the fluid strike with twice the velocity, but twice the mass of fluid strikes per second. Therefore the change of momentum per second is multiplied by four. Force is equivalent to the change of momentum divided by time. This is in contrast with solid-on-solid friction, which generally has very little velocity dependence.
dependence on velocity, meaning that fluid drag increases with the square of velocity. When velocity is doubled, for example, not only does the fluid strike with twice the velocity, but twice the mass of fluid strikes per second. Therefore the change of momentum per second is multiplied by four. Force is equivalent to the change of momentum divided by time. This is in contrast with solid-on-solid friction, which generally has very little velocity dependence.